Polarisering er en av de grunnleggende egenskapene til antenner. Vi må først forstå polariseringen av planbølger. Deretter kan vi diskutere hovedtypene av antennepolarisering.
lineær polarisering
Vi vil begynne å forstå polarisasjonen av en plan elektromagnetisk bølge.
En plan elektromagnetisk (EM) bølge har flere egenskaper. Den første er at kraften beveger seg i én retning (ingen feltendringer i to ortogonale retninger). For det andre er det elektriske feltet og magnetfeltet vinkelrett på hverandre og ortogonalt på hverandre. Elektriske og magnetiske felt er vinkelrett på retningen av plan bølgeforplantning. Som et eksempel, se på et elektrisk felt med én frekvens (E-felt) gitt ved ligning (1). Det elektromagnetiske feltet beveger seg i +z-retningen. Det elektriske feltet er rettet i +x-retningen. Magnetfeltet er i +y-retningen.
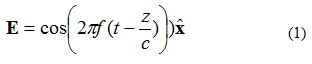
I ligning (1), legg merke til notasjonen: . Dette er en enhetsvektor (en lengdevektor), som sier at det elektriske feltpunktet er i x-retningen. Planbølgen er illustrert i figur 1.
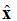
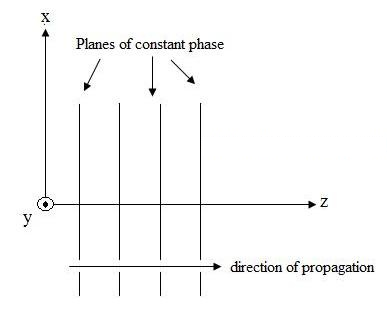
Figur 1. Grafisk fremstilling av det elektriske feltet som beveger seg i +z-retningen.
Polarisering er sporet og forplantningsformen (konturen) til et elektrisk felt. Som et eksempel kan vi se på ligningen (1) for det planbølgede elektriske feltet. Vi vil observere posisjonen der det elektriske feltet er (X,Y,Z) = (0,0,0) som en funksjon av tid. Amplituden til dette feltet er plottet i figur 2, ved flere tidspunkter. Feltet oscillerer med frekvensen "F".
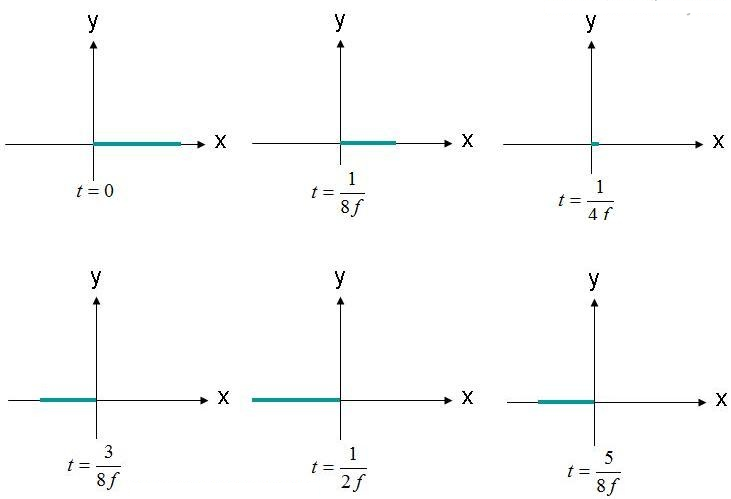
Figur 2. Observer det elektriske feltet (X, Y, Z) = (0,0,0) på forskjellige tidspunkter.
Det elektriske feltet observeres ved origo, og oscillerer frem og tilbake i amplitude. Det elektriske feltet er alltid langs den angitte x-aksen. Siden det elektriske feltet opprettholdes langs en enkelt linje, kan dette feltet sies å være lineært polarisert. I tillegg, hvis X-aksen er parallell med bakken, beskrives dette feltet også som horisontalt polarisert. Hvis feltet er orientert langs Y-aksen, kan bølgen sies å være vertikalt polarisert.
Lineært polariserte bølger trenger ikke å være rettet langs en horisontal eller vertikal akse. For eksempel vil en elektrisk feltbølge med en begrensning som ligger langs en linje som vist i figur 3 også være lineært polarisert.
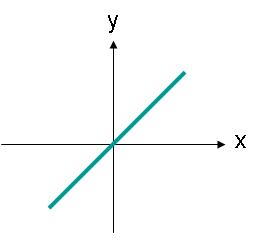
bilde 3. Den elektriske feltamplituden til en lineært polarisert bølge hvis bane er en vinkel.
Det elektriske feltet i figur 3 kan beskrives ved hjelp av ligning (2). Nå finnes det en x- og en y-komponent av det elektriske feltet. Begge komponentene er like store.
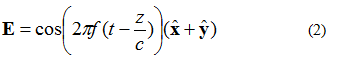
En ting å merke seg angående ligning (2) er xy-komponenten og de elektroniske feltene i det andre trinnet. Dette betyr at begge komponentene har samme amplitude til enhver tid.
sirkulær polarisering
Anta nå at det elektriske feltet til en planbølge er gitt av ligning (3):
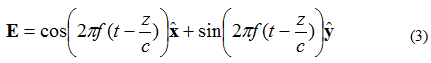
I dette tilfellet er X- og Y-elementene 90 grader ute av fase. Hvis feltet observeres som (X, Y, Z) = (0,0,0) igjen som før, vil kurven for elektrisk felt versus tid se ut som vist nedenfor i figur 4.
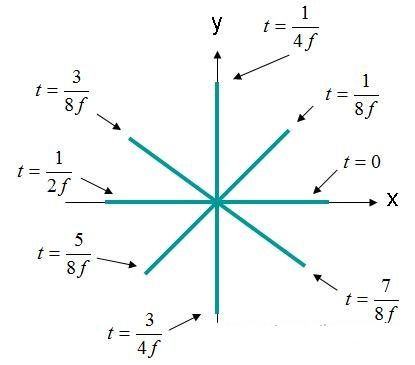
Figur 4. Elektrisk feltstyrke (X, Y, Z) = (0,0,0) EQ-domene. (3).
Det elektriske feltet i figur 4 roterer i en sirkel. Denne typen felt beskrives som en sirkulært polarisert bølge. For sirkulær polarisering må følgende kriterier være oppfylt:
- Standard for sirkulær polarisering
- Det elektriske feltet må ha to ortogonale (vinkelrette) komponenter.
- De ortogonale komponentene i det elektriske feltet må ha like amplituder.
- Kvadraturkomponentene må være 90 grader ute av fase.
Hvis man beveger seg på bølgefigur 4-skjermen, sies feltrotasjonen å være mot klokken og høyrehendt sirkulært polarisert (RHCP). Hvis feltet roteres med klokken, vil feltet være venstrehendt sirkulært polarisert (LHCP).
Elliptisk polarisering
Hvis det elektriske feltet har to vinkelrette komponenter, 90 grader ute av fase, men med lik størrelse, vil feltet være elliptisk polarisert. Betrakter vi det elektriske feltet til en planbølge som beveger seg i +z-retningen, beskrevet av ligning (4):
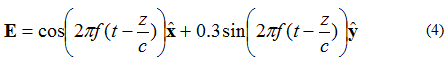
Geometrien til punktet der spissen av den elektriske feltvektoren vil innta er gitt i figur 5
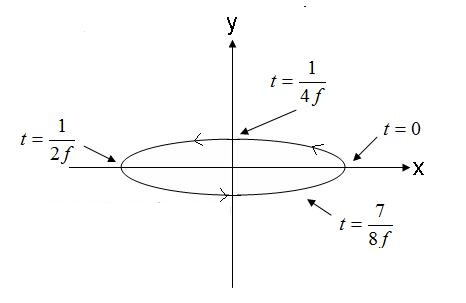
Figur 5. Prompt elliptisk polarisasjonsbølge elektrisk felt. (4).
Feltet i figur 5, som beveger seg mot klokken, ville være høyrehendt elliptisk hvis det beveger seg ut av skjermen. Hvis den elektriske feltvektoren roterer i motsatt retning, vil feltet være venstrehendt elliptisk polarisert.
Videre refererer elliptisk polarisering til dens eksentrisitet. Forholdet mellom eksentrisitet og amplitude til hoved- og biaksen. For eksempel er bølgeeksentrisiteten fra ligning (4) 1/0,3 = 3,33. Elliptisk polariserte bølger beskrives videre av retningen til hovedaksen. Bølgelkning (4) har en akse som primært består av x-aksen. Merk at hovedaksen kan være i en hvilken som helst planvinkel. Vinkelen er ikke nødvendig for å passe til X-, Y- eller Z-aksen. Til slutt er det viktig å merke seg at både sirkulær og lineær polarisering er spesialtilfeller av elliptisk polarisering. 1,0 eksentrisk elliptisk polarisert bølge er en sirkulært polarisert bølge. Elliptisk polariserte bølger med uendelig eksentrisitet. Lineært polariserte bølger.
Antennepolarisering
Nå som vi er klar over polariserte planbølge-elektromagnetiske felt, er polarisasjonen til en antenne enkelt definert.
Antennepolarisering En fjernfeltsevaluering av antennen, polariseringen av det resulterende utstrålte feltet. Derfor er antenner ofte oppført som "lineært polariserte" eller "høyrehendte sirkulært polariserte antenner".
Dette enkle konseptet er viktig for antennekommunikasjon. For det første vil ikke en horisontalt polarisert antenne kommunisere med en vertikalt polarisert antenne. På grunn av resiprositetsteoremet sender og mottar antennen på nøyaktig samme måte. Derfor sender og mottar vertikalt polariserte antenner vertikalt polariserte felt. Derfor, hvis du prøver å formidle en vertikalt polarisert horisontalt polarisert antenne, vil det ikke være mottak.
Generelt sett, for to lineært polariserte antenner rotert i forhold til hverandre med en vinkel ( ), vil effekttapet på grunn av denne polarisasjonsavviket bli beskrevet av polarisasjonstapsfaktoren (PLF):
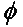
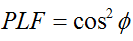
Derfor, hvis to antenner har samme polarisering, er vinkelen mellom deres utstrålende elektronfelt null, og det er ikke noe effekttap på grunn av polarisasjonsavvik. Hvis den ene antennen er vertikalt polarisert og den andre er horisontalt polarisert, er vinkelen 90 grader, og ingen effekt vil bli overført.
MERK: Å bevege telefonen over hodet i forskjellige vinkler forklarer hvorfor mottaket noen ganger kan forbedres. Mobiltelefonantenner er vanligvis lineært polariserte, så å rotere telefonen kan ofte matche polariseringen av telefonen, og dermed forbedre mottaket.
Sirkulær polarisering er en ønskelig egenskap ved mange antenner. Begge antennene er sirkulært polariserte og lider ikke av signaltap på grunn av polarisasjonsavvik. Antenner som brukes i GPS-systemer er høyresirkulært polariserte.
Anta nå at en lineært polarisert antenne mottar sirkulært polariserte bølger. Anta tilsvarende at en sirkulært polarisert antenne forsøker å motta lineært polariserte bølger. Hva er den resulterende polarisasjonstapsfaktoren?
Husk at sirkulær polarisering faktisk er to ortogonale lineært polariserte bølger, 90 grader ute av fase. Derfor vil en lineært polarisert (LP) antenne bare motta fasekomponenten av den sirkulært polariserte (CP) bølgen. Derfor vil LP-antennen ha et tap av polarisasjonsmismatch på 0,5 (-3 dB). Dette gjelder uansett hvilken vinkel LP-antennen roteres. Derfor:
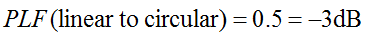
Polarisasjonstapfaktoren blir noen ganger referert til som polarisasjonseffektivitet, antennemismatchfaktor eller antennemottaksfaktor. Alle disse navnene refererer til det samme konseptet.
Publisert: 22. desember 2023







