Når det gjelderantenner, spørsmålet folk er mest opptatt av er «Hvordan oppnås egentlig stråling?» Hvordan forplanter det elektromagnetiske feltet som genereres av signalkilden seg gjennom transmisjonslinjen og inne i antennen, og til slutt «skiller» seg fra antennen for å danne en friromsbølge.
1. Enkeltrådsstråling
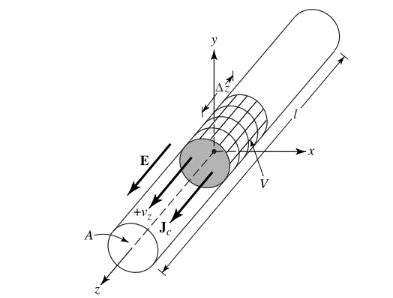
La oss anta at ladetettheten, uttrykt som qv (Coulomb/m3), er jevnt fordelt i en sirkulær ledning med et tverrsnittsareal på a og et volum på V, som vist i figur 1.
Figur 1
Den totale ladningen Q i volum V beveger seg i z-retningen med en jevn hastighet Vz (m/s). Det kan bevises at strømtettheten Jz på ledningens tverrsnitt er:
Jz = qv vz (1)
Hvis ledningen er laget av en ideell leder, er strømtettheten Js på ledningsoverflaten:
Js = qs vz (2)
Hvor qs er overflateladningstettheten. Hvis ledningen er veldig tynn (ideelt sett er radiusen 0), kan strømmen i ledningen uttrykkes som:
Iz = ql vz (3)
Hvor ql (coulomb/meter) er ladningen per lengdeenhet.
Vi er hovedsakelig opptatt av tynne ledninger, og konklusjonene gjelder for de tre tilfellene ovenfor. Hvis strømmen varierer med tiden, er den deriverte av formel (3) med hensyn til tid som følger:
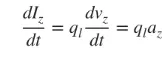
(4)
az er ladeakselerasjonen. Hvis ledningslengden er l, kan (4) skrives som følger:
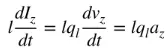
(5)
Ligning (5) er det grunnleggende forholdet mellom strøm og ladning, og også det grunnleggende forholdet for elektromagnetisk stråling. Enkelt sagt, for å produsere stråling, må det være en tidsvarierende strøm eller akselerasjon (eller retardasjon) av ladning. Vi nevner vanligvis strøm i tidsharmoniske applikasjoner, og ladning nevnes oftest i transiente applikasjoner. For å produsere ladningsakselerasjon (eller retardasjon), må ledningen være bøyd, foldet og diskontinuerlig. Når ladningen oscillerer i tidsharmonisk bevegelse, vil den også produsere periodisk ladningsakselerasjon (eller retardasjon) eller tidsvarierende strøm. Derfor:
1) Hvis ladningen ikke beveger seg, vil det ikke være noen strøm og ingen stråling.
2) Hvis ladningen beveger seg med konstant hastighet:
a. Hvis ledningen er rett og uendelig lang, er det ingen stråling.
b. Hvis ledningen er bøyd, foldet eller diskontinuerlig, som vist i figur 2, er det stråling.
3) Hvis ladningen oscillerer over tid, vil ladningen stråle ut selv om ledningen er rett.
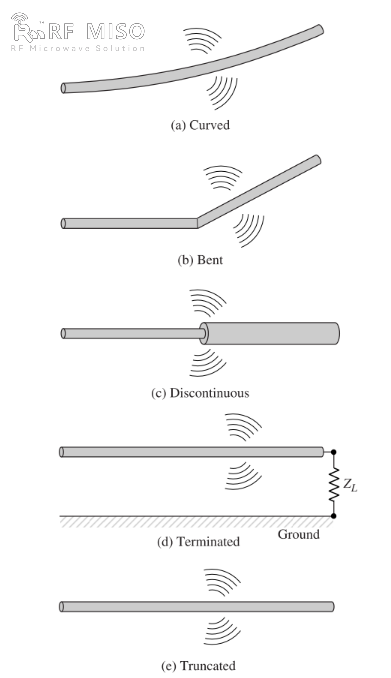
Figur 2
En kvalitativ forståelse av strålingsmekanismen kan oppnås ved å se på en pulserende kilde koblet til en åpen ledning som kan jordes gjennom en last i sin åpne ende, som vist i figur 2(d). Når ledningen først blir aktivert, settes ladningene (frie elektroner) i ledningen i bevegelse av de elektriske feltlinjene som genereres av kilden. Når ladningene akselereres ved kildeenden av ledningen og bremses ned (negativ akselerasjon i forhold til den opprinnelige bevegelsen) når de reflekteres i enden, genereres et strålingsfelt i endene og langs resten av ledningen. Akselerasjonen av ladningene oppnås av en ekstern kraftkilde som setter ladningene i bevegelse og produserer det tilhørende strålingsfeltet. Retardasjonen av ladningene i endene av ledningen oppnås av interne krefter assosiert med det induserte feltet, som er forårsaket av akkumulering av konsentrerte ladninger i endene av ledningen. De interne kreftene får energi fra akkumuleringen av ladning når hastigheten synker til null i endene av ledningen. Derfor er akselerasjonen av ladningene på grunn av eksitasjon i det elektriske feltet og retardasjonen av ladningene på grunn av diskontinuitet eller glatt kurve i ledningsimpedansen mekanismene for generering av elektromagnetisk stråling. Selv om både strømtetthet (Jc) og ladningstetthet (qv) er kildeledd i Maxwells ligninger, anses ladning å være en mer grunnleggende størrelse, spesielt for transiente felt. Selv om denne forklaringen av stråling hovedsakelig brukes for transiente tilstander, kan den også brukes til å forklare stasjonær stråling.
Anbefaler flere utmerkedeantenneprodukterprodusert avRFMISO:
2. Totrådsstråling
Koble en spenningskilde til en toleders transmisjonslinje koblet til en antenne, som vist i figur 3(a). Når man tilfører spenning til den toleders linjen, genereres et elektrisk felt mellom lederne. De elektriske feltlinjene virker på de frie elektronene (som lett kan skilles fra atomer) som er koblet til hver leder og tvinger dem til å bevege seg. Bevegelsen av ladninger genererer strøm, som igjen genererer et magnetfelt.
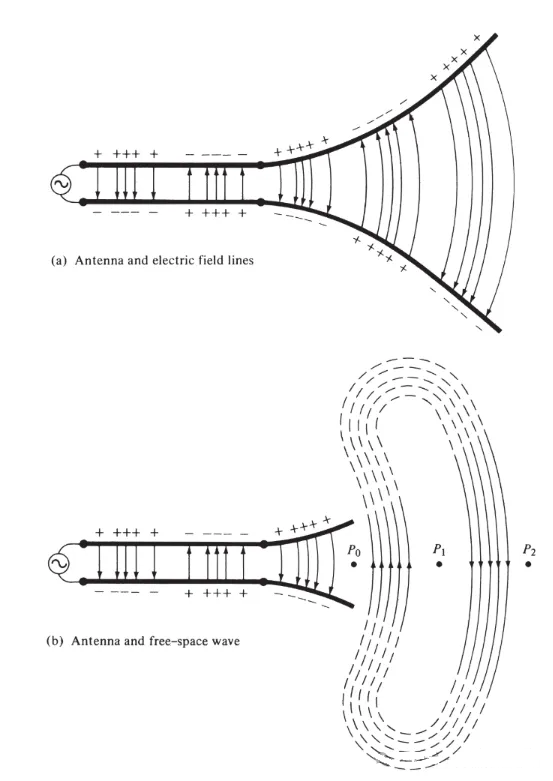
Figur 3
Vi har akseptert at elektriske feltlinjer starter med positive ladninger og slutter med negative ladninger. De kan selvfølgelig også starte med positive ladninger og slutte i uendelig; eller starte i uendelig og slutte med negative ladninger; eller danne lukkede løkker som verken starter eller slutter med noen ladninger. Magnetiske feltlinjer danner alltid lukkede løkker rundt strømførende ledere fordi det ikke finnes magnetiske ladninger i fysikken. I noen matematiske formler introduseres ekvivalente magnetiske ladninger og magnetiske strømmer for å vise dualiteten mellom løsninger som involverer kraft og magnetiske kilder.
De elektriske feltlinjene tegnet mellom to ledere bidrar til å vise ladningsfordelingen. Hvis vi antar at spenningskilden er sinusformet, forventer vi at det elektriske feltet mellom lederne også er sinusformet med en periode lik kildens. Den relative størrelsen på den elektriske feltstyrken er representert av tettheten til de elektriske feltlinjene, og pilene indikerer den relative retningen (positiv eller negativ). Genereringen av tidsvarierende elektriske og magnetiske felt mellom lederne danner en elektromagnetisk bølge som forplanter seg langs transmisjonslinjen, som vist i figur 3(a). Den elektromagnetiske bølgen kommer inn i antennen med ladningen og den tilsvarende strømmen. Hvis vi fjerner en del av antennestrukturen, som vist i figur 3(b), kan en friromsbølge dannes ved å "koble sammen" de åpne endene av de elektriske feltlinjene (vist med de stiplede linjene). Friromsbølgen er også periodisk, men konstantfasepunktet P0 beveger seg utover med lysets hastighet og tilbakelegger en avstand på λ/2 (til P1) i løpet av en halv tidsperiode. Nær antennen beveger konstantfasepunktet P0 seg raskere enn lysets hastighet og nærmer seg lysets hastighet på punkter langt fra antennen. Figur 4 viser fordelingen av det frie elektriske felt for λ∕2-antennen ved t = 0, t/8, t/4 og 3T/8.
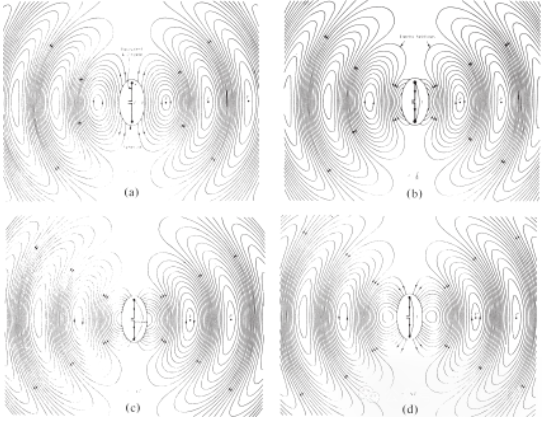
Figur 4 Fordeling av elektrisk felt i fritt rom for λ∕2-antennen ved t = 0, t/8, t/4 og 3T/8
Det er ikke kjent hvordan de styrte bølgene skilles fra antennen og til slutt dannes for å forplante seg i det frie rom. Vi kan sammenligne styrte og frie rombølger med vannbølger, som kan være forårsaket av en stein som slippes i et rolig vann eller på andre måter. Når forstyrrelsen i vannet begynner, genereres vannbølger som begynner å forplante seg utover. Selv om forstyrrelsen stopper, stopper ikke bølgene, men fortsetter å forplante seg fremover. Hvis forstyrrelsen vedvarer, genereres det stadig nye bølger, og forplantningen av disse bølgene henger etter de andre bølgene.
Det samme gjelder for elektromagnetiske bølger generert av elektriske forstyrrelser. Hvis den første elektriske forstyrrelsen fra kilden er av kort varighet, forplanter de genererte elektromagnetiske bølgene seg inne i transmisjonslinjen, går deretter inn i antennen og stråler til slutt ut som friromsbølger, selv om eksitasjonen ikke lenger er tilstede (akkurat som vannbølgene og forstyrrelsen de skapte). Hvis den elektriske forstyrrelsen er kontinuerlig, eksisterer de elektromagnetiske bølgene kontinuerlig og følger tett bak dem under forplantningen, som vist i den bikoniske antennen vist i figur 5. Når elektromagnetiske bølger er inne i transmisjonslinjer og antenner, er deres eksistens relatert til eksistensen av elektrisk ladning inne i lederen. Men når bølgene utstråles, danner de en lukket sløyfe, og det er ingen ladning som opprettholder deres eksistens. Dette leder oss til konklusjonen at:
Eksitering av feltet krever akselerasjon og retardasjon av ladningen, men opprettholdelse av feltet krever ikke akselerasjon og retardasjon av ladningen.
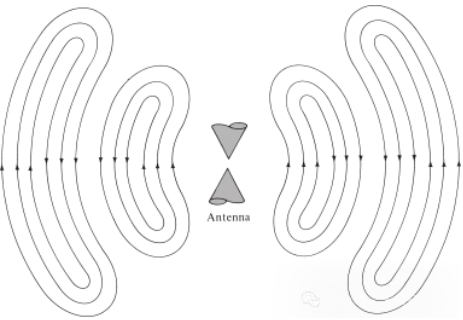
Figur 5
3. Dipolstråling
Vi prøver å forklare mekanismen som gjør at de elektriske feltlinjene bryter løs fra antennen og danner friromsbølger, og tar dipolantennen som et eksempel. Selv om det er en forenklet forklaring, gjør den det også mulig for folk å intuitivt se genereringen av friromsbølger. Figur 6(a) viser de elektriske feltlinjene som genereres mellom de to armene på dipolen når de elektriske feltlinjene beveger seg utover med λ∕4 i første kvartal av syklusen. La oss for dette eksemplet anta at antallet dannede elektriske feltlinjer er 3. I neste kvartal av syklusen beveger de opprinnelige tre elektriske feltlinjene seg ytterligere λ∕4 (totalt λ∕2 fra startpunktet), og ladningstettheten på lederen begynner å avta. Den kan anses å være dannet ved introduksjon av motsatte ladninger, som kansellerer ut ladningene på lederen på slutten av første halvdel av syklusen. De elektriske feltlinjene som genereres av de motsatte ladningene er 3 og beveger seg en avstand på λ∕4, som er representert av de stiplede linjene i figur 6(b).
Det endelige resultatet er at det er tre nedadgående elektriske feltlinjer i den første λ∕4-avstanden og samme antall oppadgående elektriske feltlinjer i den andre λ∕4-avstanden. Siden det ikke er noen nettoladning på antennen, må de elektriske feltlinjene tvinges til å skille seg fra lederen og kombineres for å danne en lukket sløyfe. Dette er vist i figur 6(c). I den andre halvdelen følges den samme fysiske prosessen, men merk at retningen er motsatt. Etter det gjentas prosessen og fortsetter i det uendelige, og danner en elektrisk feltfordeling som ligner på figur 4.
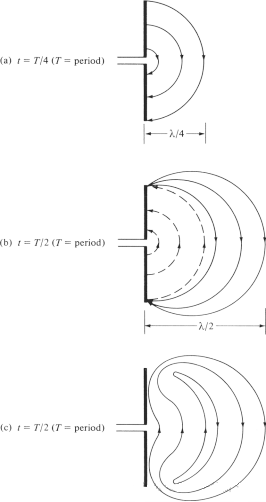
Figur 6
For å lære mer om antenner, vennligst besøk:
Publisert: 20. juni 2024










